Yes, prime numbers are a go-to challenge for me that I’ve been casually playing with since my earliest programming days. I’m not alone; prime numbers are important and popular enough that there’s an entire distributed computing project dedicated to finding the highest Mersenne Prime number (primes such as 31 and 127 that are one less than a power of 2). A decent grounding in math is also important for programmers and prime number algorithms are a much better programming exercise than “Hello, World”.
That’s why, during a holiday trip to a local Barnes & Noble, I was looking through their collection of quick and shallow knowledge books (“100 Factoids That Will Make You Sound Knowledgeable …” ) and found one called Math Squared: 100 Concepts You Should Know. I wasn’t expecting a degree out of this small, 256-page book but it’s been awhile since math class, I thought it might give me some good ideas for programming exercises and I like the feel and smell of new books.
The book really does give a five-minute intro to each subject at most but a short ways into the first chapter, I stumbled upon a fact I should have realized before. That is that every prime number is either one less or one more than a multiple of 6. This makes a lot of sense when you really look at an example. Excuse me while I geek out a little over the math:
5 - Prime 6 - Multiple of 6 7 - Prime 8 - Even (divisible by 2) 9 - Divisible by 3 10 - Even 11 - Prime 12 - Multiple of 6 13 - Prime
Again, a prime number is only divisible by itself and 1. There are five numbers between each multiple of 6, the third number will always be divisible by 3 and therefore is not a prime. Then you knock out the even numbers which are divisible by 2 and the only numbers left that can be prime are those on either side of the multiple. That does not mean that every number over and under a multiple of 6 is prime; a number like 25 ((6×4) + 1) is divisible by five. Still, if you want to find primes, that’s where you could start looking.
That gave me a new idea for a prime algorithm. I’ve always used variations of the brute force method that divides a number by whole numbers from 2 to the square root of the number being tested to determine if there are any other factors (i.e. divide 121 by numbers from 2 to 11 – it’s divisible by its own square root of 11 and therefore is not prime). As you get into the tens of millions, the process slows down quite a bit as each candidate number has to be tested against hundreds and eventually thousands of other numbers. Even with a really good algorithm, the fastest PC starts to bog down after awhile. That’s why the Mersenne project has been going for years.
Here’s a really basic, and fairly slow, algorithm in C#:
private static bool primeTest(long primeCandidate){
bool outResult = true;
for (long x = 2; x <= Math.Sqrt(primeCandidate); x++){
if (primeCandidate % x == 0){
outResult = false;
break;
}
}
return outResult;
}
The function starts by assuming prime and tests the number by every number from 2 to the integer of the candidate’s square root.
So, armed with this new factoid, I thought “What if I just test the numbers on each side of the multipliers of 6?” That should eliminate a lot of unnecessary calculations and speed things up. Here’s an example that calls the function above where the main purpose is to find the highest prime number up to a set limit.
private static long PrimesBySix(long upperLimit){
long primeBase = 6;
long highPrime = 0;
while (primeBase <= upperLimit){
if (primeTest(primeBase - 1))
highPrime = primeBase - 1;
if (primeTest(primeBase + 1))
highPrime = primeBase + 1;
primeBase += 6;
}
return highPrime;
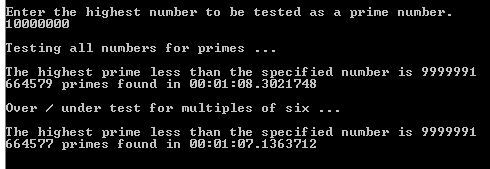
This worked but I needed to know if it was really much more efficient than testing every all numbers or every odd number. For a dramatic demonstration, we can put it up against a really basic routine and have each routine test prime candidates up to ten million. Each function returns a list of the primes so the highest prime number and the number of primes returned can be verified.
The second test started testing with 6 so it did not find the primes of 3 and 5, hence the difference in the number of primes. As you can see, there’s virtually no difference in the performance which surprised me the first time I ran this and before I worked out why all the primes are hanging around the multiples of six as I explained above.
The fact is that the over / under test above would be a great time saver for a human but it doesn’t eliminate that much work for the program. When testing all numbers for prime, the even numbers and those divisible by 3 are eliminated in only one or two iterations and the program moves on to the next candidate. Then the over / under test loses a bit of the savings it does get by finding the candidates on either side of each multiple of six.
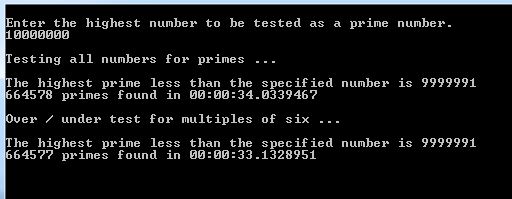
Now let’s look at the results of fixing the prime testing algorithm itself to match the one below which eliminates all even numbered candidates and only throws odd numbers against the remaining candidates.
private static bool primeTest(long primeCandidate){
bool outResult = true;
if (primeCandidate % 2 == 0)
outResult = false;
if (outResult){
for (long x = 3; x <= Math.Sqrt(primeCandidate); x += 2){
if (primeCandidate % x == 0){
outResult = false;
break;
}
}
}
return outResult;
}
… and there’s the real performance boost. Reducing the number of candidates being passed to the testing routine saved virtually no time in either test but improving the algorithm by which those candidates were evaluated made all the difference. The processing time was cut in half because the heart of the process was made more efficient and its work was reduced by half. The bottleneck was not in the expected place.
There’s no substitute for a good algorithm and the willingness to put your code to the test.
Find related products on Amazon.com ...






![STEP UP YOUR PRINTING GAME. KODAK Step Printer Connects to Any iOS or Android Device [Via Bluetooth or NFC] Turn Your Selfies, Portraits, Social Media Posts Into Physical Photos AMAZING ZERO-INK TECHNOLOGY. ZINK 2” x 3” Sticky-Back Paper with Embedde...](https://m.media-amazon.com/images/I/41gY+-0dajL._SL250_.jpg)




